Third Post of a Series of 4
This post is the third of a series of 4 about the information rate that can be transported by submarine cable systems. The first post of this series presented in a simple way the Shannon limit that drives the ultimate subsea cable system capacity. The second post examined the various multiplexing options that can be put at work for increasing subsea cable system capacity and lowering the cost per transported bit as well. This post looks at some technologies that can be used to get closer to the Shannon limit with the objective of maximizing the capacity transported by a single communication channel (in our case, a single fiber core). Finally, the fourth post will review the most recent and significant results from laboratory demonstrations and field trials so one can get a good view of what will be feasible, capacity wise, in the short-and mid-terms.
Getting Closer to the Shannon Limit
Three conditions are required to approach the Shannon limit:
- Nyquist Pulses – Nyquist optical pulses should be used for playing with Inter-Symbol Interference (ISI) free signal. Ideal Nyquist pulse strings lead to zero ISI at the sampling points if the receiver synchronization is perfectly carried out. In the spectral domain, an ideal Nyquist pulse string results into a raised cosine optical spectrum with β coefficient that can be as low as 0.001; such a low β coefficient provides quasi-rectangular spectrum with minimal spectral occupancy, allowing many optical carriers to be packed within a given optical spectrum (as imposed by the optical amplifier technology used in the submerged repeaters).
- Error-Correcting Code – Coding data for detecting long sequences of bits, detecting/correcting errors and lowering bit error rate. Claude Shannon demonstrated that for any communication channel, there must be an error-correcting code that enables transmissions to approach the Shannon limit. Forward Error Correction (FEC) coding is an active R&D field with the recent introduction of soft-decision and adaptive-rate FEC decoding technologies.
- Two-Dimension Gaussian Distribution Across Symbol Constellation – In coherent transmission systems, the information is coded in the amplitude and phase of the optical pulses launched into the optical fiber. Multi-level modulation formats with two-dimension Gaussian distribution of the in-phase and quadrature symbols enable operation close to the Shannon limit. In other words, the symbol patterns effectively launched into the fiber should use often low-amplitude symbols and rarely high-amplitude symbols. A two-dimension Gaussian distribution can be achieved in different ways, one of them being constellation shaping.
This post will focus on constellation shaping as we are seeing more and more proposals based on this approach for increasing the fiber spectral efficiency and getting closer to the Shannon limit.
Before Constellation Shaping
In most cases, the mapping table, which maps blocks of incoming information bits to the symbols to be transmitted, is such that the Probability Mass Function (PMF) of symbols over the constellation points is a uniform distribution (in other words, the symbols are equiprobable). Probability reminder: a probability mass function is a function that gives the probability that a discrete random variable (like a symbol from a 2mQAM constellation chart) is exactly equal to some value.
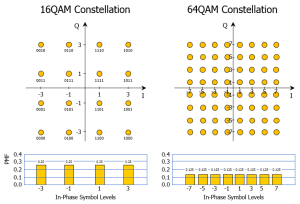
If we take the example of a 16QAM modulation format in the figure below, the constellation is made of 16 symbols. Four bits are encoded into each symbol. The mapping law is the mechanism that assigns each block of four data bits to a symbol of the constellation. For instance, the 1011 four-bit block is assigned to the (3; 1) symbol in the figure below. In a conventional 16QAM constellation, each of the 16 symbols has an equal chance of being assigned and transmitted. The PMF of each of the four possible in-phase symbol levels is therefore 0.25 (with, of course, the sum of the PMF of the four in-phase symbols being equal to 1). Moving to a 64QAM modulation format, the constellation is made of 64 symbols, each of them having an equal chance of being transmitted. Consequently, the PMF of each of the eight possible in-phase symbol levels is 0.125 (with 8 x 0.125 = 1), as shown on the right side of the picture below.
What Is Constellation Shaping?
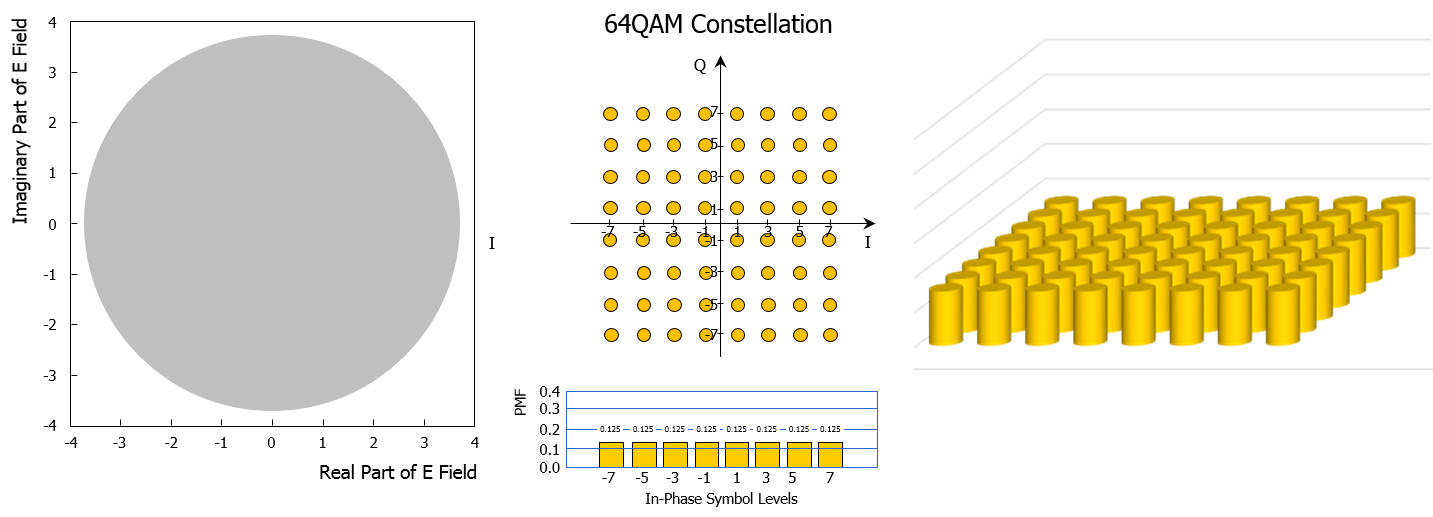
It has been shown that the gap between the practically achieved capacity and the theoretically achievable Shannon’s capacity is reduced if the modulation format exhibits a two-dimension Gaussian probability mass function for both the in-phase and quadrature components of the constellation symbols. In other words, the optical link can be operated closer to the Shannon limit if the discrete symbol source statistics looks more “Gaussian”, i.e. if the symbols located in the center of the constellation are the more likely to occur.
The probability mass function of a “simple” discrete source of symbols is by essence not Gaussian (see the PMF of the in-phase symbol levels that are flat over the level range for standard 16QAM and 64QAM constellations as represented in the above figure). Consequently, standard 64QAM modulation format as depicted below are sub-optimal and do not enable to get very close to the Shannon’s capacity limit, even with the most sophisticated error-correction codes.
Constellation shaping techniques are an ensemble of various techniques to turn constellations with equidistant, equiprobable symbols (like standard square 16QAM or 64QAM constellations) into more “Gaussian” constellations. Probabilistic Shaping (PS) and Geometric Shaping (GS) are the two main options to mimic a “Gaussian-like” shape of the constellation.
Probabilistic Constellation Shaping
Probabilistic shaping imposes a non-uniform distribution (i.e. non equiprobable symbols) on a set of equidistant constellation points. Probabilistic shaping relies on the use of a code (called distribution matcher) to gradually vary the probability distribution of the constellation points (from higher probability for the innermost constellation points, to lower probability for the outermost constellation points), resulting in probabilistic shaping of the constellation. Probabilistic shaping can be applied to any constellation type, including 64QAM constellation as shown in the figure below, with a non-equally probability distribution of the individual constellation points: the inner constellation points carrying a lower energy are used with higher probability while the outer constellation points carrying a higher energy are used with lower probability. The probabilities are typically taken from the Maxwell-Boltzmann distribution family and applied independently to both the in-phase and quadrature components of the QAM signal.
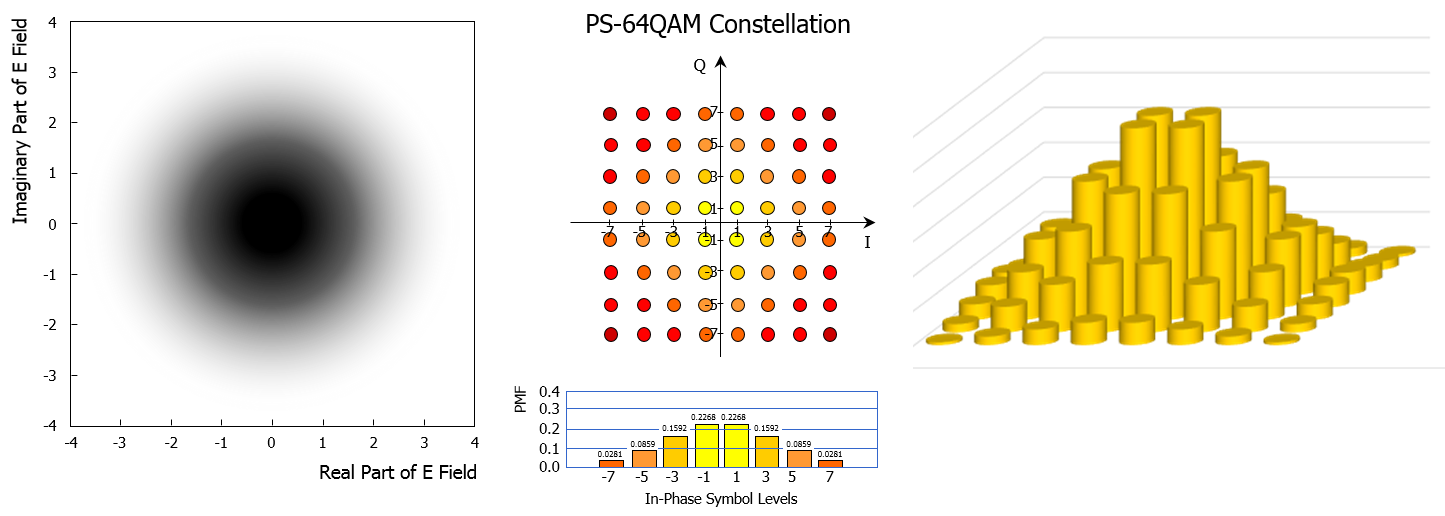
A standard 64 QAM modulator is used for building a PS-64QAM constellation; the probabilistic shaping of the constellation is built by a specific device, the so-called distribution matcher. The input of the distribution matcher is made of the uniformly data bits that need to be transported; the output of the distribution matcher delivers a non-uniform stream of, e.g., in-phase symbol levels from the {1,3,5,7} alphabet, resulting into probabilistically shaped symbol levels. Probabilistic shaping with adjustable distributions has been proposed to enable flexible spectral efficiency and/or bit rate.
Geometric Constellation Shaping
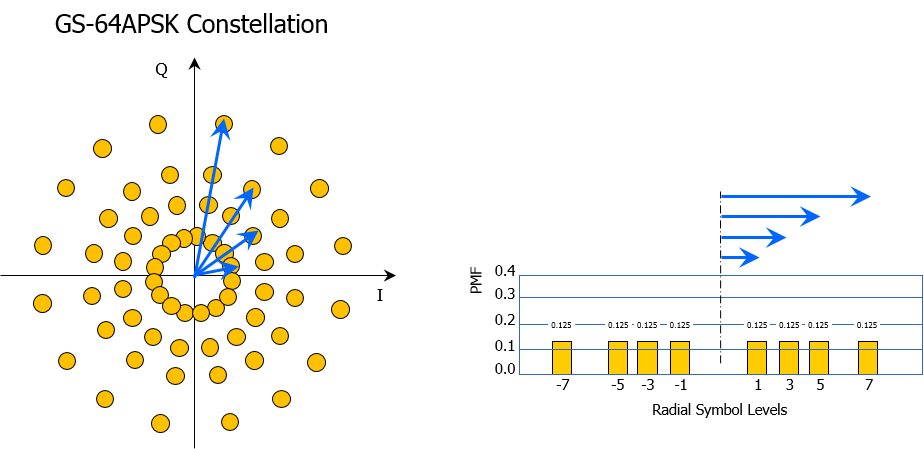
Geometric shaping employs a uniform distribution (i.e. equiprobable symbols) on non-equidistant constellation points; this represents a change in the standard square 2mQAM constellation. In Geometric Shaping (GS) constellation (like the GS-64APSK modulation represented below), the symbols are by definition not uniformally spaced across the constellation. The in-phase symbols depend on the quadrature symbols and there is no independent processing of in-phase and quadrature symbols; geometric shaping usually results in more complex modulation and decoding schemes contrary to probabilistic shaping which is based on pragmatic square QAM modulation scheme.
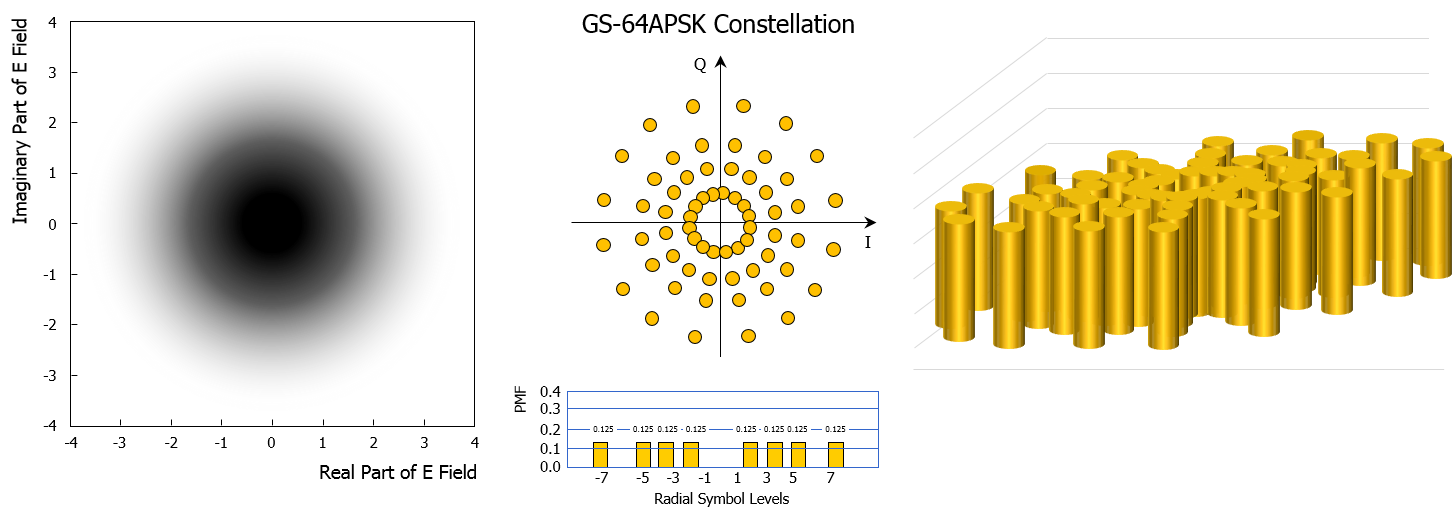
Geometric constellation shaping is typically based on ring constellations denoted as Amplitude and Phase-Shift Keying or Asymmetric Phase-Shift Keying (APSK). This is a digital modulation scheme that still conveys data by modulating both the amplitude and the phase of the optical carrier wave but with a smaller number of possible amplitude levels than found in QAM modulation scheme. This is illustrated in the figure below for a 16-symbol modulation: a 16QAM constellation requires three different amplitude levels while a 16APSK constellation is based on two levels.

With more amplitude levels, geometric shaping is achieved by increasing in a nonlinear way the radius of the different symbol rings starting from the constellation center: this is how the two-dimension Gaussian distribution of constellation symbols is emulated. More symbols are found near the constellation center than at its periphery: even if all the symbols are equiprobable, the two-dimension distribution of symbol occurrence will look like a “Gaussian” one.
Hybrid Constellation Shaping, Best of Both Worlds?
Some experimental works were based on constellation shaping done both geometrically and probabilistically. In a TE SubCom technical paper presented at OFC 2017 conference (70.4 Tb/s Capacity over 7,600 km in C+L Band Using Coded Modulation with Hybrid Constellation Shaping and Nonlinearity Compensation, by J. -X. Cai et al.), 56APSK constellation was used as shown in the figure below. As described in TE SubCom’s paper, this format is based on a specific code to gradually vary the probability distribution of the constellation points from 16 equiprobable points on the outer ring to 8 equiprobable points on the inner ring, resulting in 56 constellation points. In addition to this geometric shaping, which is achieved by selecting a particular ring-based constellation and by optimizing the radii of the 4 rings, probabilistic shaping is used as well. This is visible in the figure below where the yellow symbols are the most likely to be transmitted while the red symbols are those that are the least likely to be transmitted. Given that the shaping is done both geometrically and probabilistically, this constellation shaping is referred as Hybrid Shaping (HS), with non-uniform distribution (i.e. non equiprobable symbols) on non-equidistant constellation points.

The next post (and last one of this series) will review the most recent and significant laboratory demonstrations and field trials to provide a good view of what will be feasible, capacity wise, in the short-and mid-terms.
For comments or questions, please contact us.